[CNDT] - Khám phá quy tắc đại số trước khi đếm 1, 2, 3, 4... (Phần 2)

Khởi đầu hành trình toán học bằng phép đếm và số tự nhiên cũng là truyền thống dạy và học toán ở nhiều nước trên thế giới. Dưới ánh sáng khoa học hiện đại, cách tiếp cận này có những ưu nhược điểm gì về mặt giáo dục, nhận thức? Và đây có phải là cách duy nhất để xây dựng những khái niệm toán học đầu tiên cho học sinh lớp 1?

Mời bạn đọc đến với phần 2 của loạt bài về tư duy toán học và phương pháp mới giúp học sinh phát triển tư duy đại số. Loạt bài thể hiện góc nhìn của Keith Devlin, nhà toán học nổi tiếng thế giới là cựu giáo sư toán đại học Stanford.

Phần 2: Bắt đầu môn toán, học đếm trước hay đo lường trước?

Một cách khác để đặt nền móng cho lâu đài toán học

Chúng ta biết rằng tổ tiên chúng ta bắt đầu đếm các loại cổ vật khác nhau như dấu chữ V trên que và xương, phác thảo trên các bức tường hang động, các đống đá sỏi… ít nhất là cách đây 35 ngàn năm, tiến tới các vật đại diện phức tạp hơn như đất sét của người Sumer cách đây 8 ngàn năm, sự xuất hiện của các con số trừu tượng và những ký hiệu viết để mô tả chúng cách đây khoảng 6-7 ngàn năm. Sự phát triển này dẫn tới các số nguyên dương với phép cộng và cuối cùng là số hữu tỉ với phép cộng, sự phát triển mà chúng tôi nghĩ là do thương mại-ham muốn/nhu cầu theo dõi tài sản và mua bán với người khác của các tộc người.

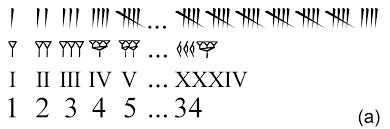
Qua các bằng chứng khảo cổ, ta cũng thấy rõ là tổ tiên chúng ta đã phát triển các hệ thống đo lường chiều dài và diện tích để đo đạc đất đai, vụ mùa cây trồng, thiết kế và xây dựng các tòa nhà. Từ góc nhìn hiện đại, điều này thật giống với cách bắt đầu hệ thống số thực, dù vẫn chưa rõ là vào lúc nào thì các hoạt động đó trở thành các con số như mức độ mà chúng ta nhận thức được hôm nay.

Dường như, khi hướng dẫn trẻ em đi những bước đầu tiên trên con đường dài đến với tư duy toán học dựa trên trải nghiệm hàng ngày và năng lực nhận thức con người, có hai cách khả thi để bắt đầu: thế giới rời rạc gồm kích thước các tập hợp và thế giới liên tục các độ dài và thể tích. Cách đầu dẫn tới các số tự nhiên và phép đếm, còn cách thứ hai dẫn tới số thực và phép đo.

Giáo trình toán Mỹ hiện nay bắt đầu theo cách thứ nhất: đi theo trật tự tuyến tính từ các số nguyên dương và phép cộng tới các số âm, số hữu tỉ rồi hệ thống số thực như đích đến của quá trình nghiên cứu. Cách này làm nảy sinh giả định là các số tự nhiên cơ bản hay tự nhiên hơn các số thực.

Tuy vậy, đó không phải là cách mọi thứ được tiết lộ về mặt lịch sử. Nếu bạn xây dựng số thực từ số tự nhiên, bạn sẽ đối mặt với một tiến trình dài và phức tạp đã khiến các nhà toán học mất 2000 năm để hoàn thành nhiệm vụ vào cuối thế kỷ 19. Điều này cũng không có nghĩa là số thực là một khái niệm khó nắm bắt hơn số tự nhiên về mặt nhận thức, hay cái này tạo nên cái kia về mặt nhận thức. Con người có năng khiếu tự nhiên để khái quát hóa các số đếm rời rạc từ trải nghiệm hàng ngày (kích cỡ các nhóm vật thể rời rạc) lẫn cảm giác tự nhiên về các đại lượng liên tục như độ dài và thể tích (diện tích thì kém tự nhiên hơn) và sự khái quát hóa trong lĩnh vực này dẫn tới các số thực dương.

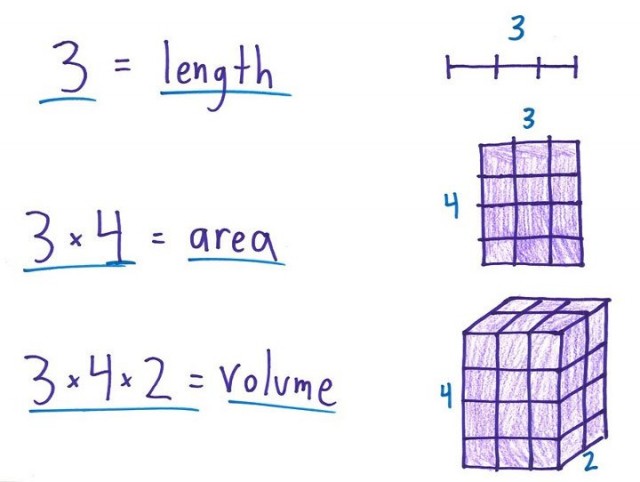
Nói cách khác, trái với quan điểm toán học, từ quan điểm nhận thức, số tự nhiên không có tính nền tảng hay tự nhiên hơn số thực. Chúng đều nảy sinh trực tiếp từ trải nghiệm trong thế giới hàng ngày của chúng ta. Hơn nữa, chúng trỗi dậy song song từ các tiến trình nhận thức khác nhau, được dùng cho các mục đích khác nhau mà không phụ thuộc vào nhau.

Trên thực tế, có rất ít bằng chứng từ ngành sinh lý học thần kinh hiện tại cho thấy số thực-cảm nhận về số liên tục-lại cơ bản hơn số tự nhiên được xây dựng dựa trên cảm nhận số liên tục bằng năng lực ngôn ngữ của chúng ta. Để biết thêm chi tiết, bạn hãy tìm đọc các sách và bài báo gần đây của các nhà nghiên cứu như Stanislaw Dehaene (tác giả, nhà thần kinh học nhận thức người Pháp) hay Brian Butterworth (nhà tâm lý học thần kinh nổi tiếng người Anh nghiên cứu nhiều lĩnh vực, trong đó có tâm lý toán học).

Nền tảng nào tốt hơn?

Nếu chúng ta bắt đầu bằng phép đo, các số đếm và số hữu tỉ dương sẽ nảy sinh như các điểm đặc biệt trên trục số liên tục. Còn bắt đầu bằng phép đếm thì các số thực sẽ nảy sinh bằng cách "lấp đầy chỗ trống" trên trục số hữu tỉ. Và trong cả hai trường hợp, bạn đều phải xoay sở với các số âm tốt nhất có thể khi nhu cầu nảy sinh.

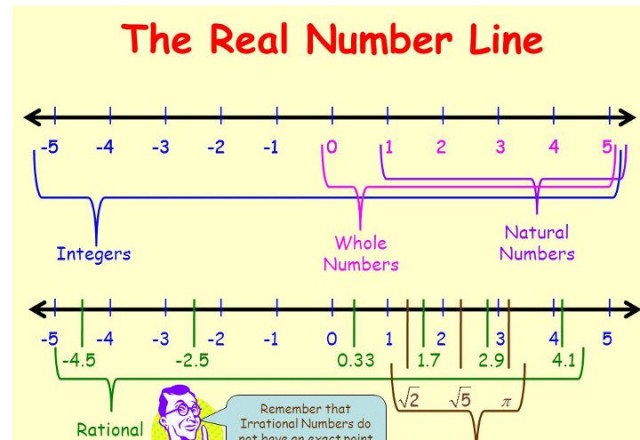
Từ góc độ học tập, không có phương pháp nào đem lại những lợi thế quan trọng so với phương pháp kia. Hãy lựa chọn và sống với các hệ quả khi lựa chọn giáo trình tương ứng.

Đúng là về mặt toán học thì việc xây dựng khái niệm số thực từ số tự nhiên khó hơn nhiều là nhận ra số tự nhiên và số hữu tỉ trên trục số thực, nhưng vấn đề ở đây không phải là xây dựng toán học có tính hình thức mà vấn đề là nhận thức con người dựa trên kinh nghiệm hàng ngày.
 

Tại Mỹ và nhiều quốc gia khác, xưa nay các giáo viên luôn chọn bắt đầu giảng dạy môn toán bằng phép đếm, và điểm khởi đầu của hành trình toán học là số tự nhiên. Nhưng có ít nhất một cố gắng nghiêm túc để thiết kế nên một giáo trình toán hoàn toàn theo phương pháp kia, và đó là trọng tâm trong phần còn lại của bài viết này. Không chỉ vì tôi nghĩ cách này tốt hơn cách kia về bản chất mà là vì, dù ứng dụng cách thức nào thì nhiều khả năng là chúng ta sẽ làm việc tốt hơn và hiểu rõ hơn những gì chúng ta đang làm trong công việc giáo viên, nếu chúng ta ý thức về một cách tiếp cận thay thế.

Thật sự, kiến thức về một cách tiếp cận khác có thể giúp chúng ta dẫn dắt học sinh qua những lĩnh vực hóc búa như khái niệm phép nhân, chủ đề của một bài viết cũ trong mục này của tôi (mục Devlin's Angle trên website Hiệp hội toán Mỹ - MAA). Theo Piaget và những người khác cũng đã đề cập khá nhiều, giúp học sinh hiểu rõ phép nhân trong giáo trình bằt đầu bằng phép đếm là cực kỳ khó. Còn giáo trình bắt đầu bằng phép đo thì ngược lại, đơn giản là vì những phức tạp gai góc gây phiền toái của phép nhân khi đếm số không xuất hiện.

Jean Piaget (1896-1980) là nhà tâm lý học Thụy Sĩ nổi tiếng trong thế kỷ 20, người có nhiều đóng góp quan trọng cho các lý thuyết phát triển nhận thức ở trẻ em và thuyết học tập kiến tạo. Học tập kiến tạo (constructivism) xem việc học là một quá trình xây dựng tích cực. Người học tích lũy kiến thức dựa trên trải nghiệm cá nhân và việc ứng dụng kiến thức mới vào thực tiễn thay vì thụ động tiếp nhận kiến thức như cách học truyền thống.

Có thể con đường phía trước để thành công hơn trong giáo dục toán học sớm là ứng dụng một cách tiếp cận lai, xây dựng khái niệm dựa trên cả hai sự trực nhận của con người cùng lúc?

Tôi cho là, dù thế nào thì điều này cũng có thể xảy ra ở mức độ nào đó. Trẻ em Mỹ bắt đầu bằng phép đếm cũng sử dụng độ dài, thể tích và các phép đo số thực khác trong cuộc sống của chúng, và trẻ em bắt đầu bằng phép đo chắc chắn có thể đếm, cộng và trừ các số tự nhiên trước khi đến trường. Nhưng tôi không ý thức về một giáo trình học chính quy nào cố gắng kết hợp cả hai cách tiếp cận này.

Dù cách tiếp cận nào trong hai cách trên được áp dụng thì mục tiêu chủ yếu của 12 năm học toán trên thế giới hiện nay đều giống nhau: trang bị cho các công dân tương lai hiểu biết về số thực và sự vận dụng thành thạo các quy tắc (procedural fluency) với số thực. Trong hệ thống trường học Mỹ, điều này được thực hiện theo cách phát triển từ các giai đoạn đầu là số tự nhiên, số nguyên, số hữu tỉ trong môn "số học" và số thực trong môn "đại số".
Cần lưu ý rằng việc để số thực trong phạm vi môn "đại số" theo cách tiếp cận Mỹ là để đảm bảo cho một biện pháp hoàn toàn mang tính thủ tục, né tránh rất nhiều khó khăn liên quan đến việc xây dựng khái niệm số thực từ số hữu tỉ. Vậy là, cuối cùng thì phương pháp bắt đầu bằng đếm số cũng phải dựa vào sự trực nhận và kinh nghiệm hàng ngày của chúng ta với các phép đo lường liên tục.